Il y a moins de force gravitationnelle, mais de combien? Une quantité insignifiante.La force d'attraction gravitationnelle entre deux objets est donnée par,

$ \ displaystyle F _ {\ mathrm g} = \ frac {G m_ {1} m_ {2}} {R ^ 2 } $,

où,

$ G $ est la constante gravitationnelle,

$ R $ est la distance entre les centres de l'objet, et

$ m_ {1} $ et $ m_ {2} $ sont les masses des objets.

Au lieu de trouver la variation de force entre l'avion et la terre, il vaudrait mieux trouver la variation de l'accélération due à la gravité, $ g $ (as $ F _ {\ mathrm g} = m _ {\ mathrm a} g $, avec $ m _ {\ mathrm a} $ étant la masse de l'avion de ligne)

Nous avons, sur la surface de la terre,

$ \ displaystyle g = \ frac {G m _ {\ mathrm e}} {R _ {\ mathrm e} ^ 2} $

où,

$ m _ {\ mathrm e} $ est la masse de la terre, et

$ R _ {\ mathrm e} $ est le rayon de la terre.

Pour l'avion à une altitude $ h $ au-dessus de la surface de la terre, cela devient,

$ \ displaystyle g_ {h} = \ frac {G m _ {\ mathrm e} } {\ left (R _ {\ mathrm e} + h \ right) ^ 2} $

En prenant le ratio, nous get,

$ \ displaystyle \ frac {g_ {h}} {g} = \ left (1 + \ frac {h} {R_ {e}} \ right) ^ {- 2} $

En branchant les chiffres, on obtient, pour un avion de ligne naviguant à 12 km,

$ g_ {h} = 9.773 \ \ mathrm {m \ s ^ {- 2}} $,

soit environ 0,37% de moins par rapport à la valeur du niveau de la mer. C'est assez petit et ne serait pas perceptible pour tous sauf les instruments sensibles.

La gravité elle-même

@aeronalias a tout à fait raison. Compte tenu de l'accélération gravitationnelle de $ g = 9.81m / s ^ 2 $ au sol, une terre sphérique parfaite de rayon $ R_E = 6370km $ de densité homogène (au moins: radialement symétrique), on peut calculer l'accélération gravitationnelle à une altitude de $ h = 12km $ par

$$ g (h) = g \ cdot \ frac {R_E ^ 2} {(h + R_E) ^ 2} = 9.773 \ rm {m} / s ^ 2 $$

Exprimée en termes de $ g $, la différence est

$$ g_ \ rm {diff} = 0,0368565736 m / s ^ 2 = 0,003757g $$

Forces centrifuges

La question demande également l’effet centrifuge sur l’avion lorsqu’il parcourt la courbe de la terre , auquel il n’a pas encore été répondu. L'effet est considéré comme petit, mais comparé à l'effet sur la gravité elle-même, ce n'est pas toujours le cas.

J'ai de lourdes objections sur ma réponse et je dois admettre que je ne vois vraiment pas leur point . Par conséquent, j'ai édité cette section et j'espère que cela vous aidera.

En général, un objet se déplaçant sur une trajectoire circulaire subit une accélération centrifuge, pointant loin du centre du cercle:

$$ a_c = \ omega ^ 2r = \ frac {v ^ 2} {r} $$

$ \ omega = \ frac {\ alpha} {t} $ est la vitesse angulaire, c'est-à-dire la angle $ \ alpha $ (en radians) l'objet se déplace dans un temps donné $ t $ (en secondes).

Considérons maintenant une Terre "parfaite" comme décrit ci-dessus, plus aucun vent. stationnaire sur un point de l'équateur à 12 km d'altitude fera un tour ($ \ alpha = 2 \ pi [= 360 °] $) en 24 heures. C'est donc $ \ omega = \ frac {2 \ pi} {24 \ cdot60 \ cdot60s} $. Avec $ r = R_e + h $, on obtient pour le ballon:

$$ a_ {cb} = 0,03374061 m / s² = 0,0034394098 g $$

La circonférence du cercle le ballon vole est $ 2 \ pi (R_e + h) = 40099km $

Considérons maintenant un avion volant vers l'est le long de l'équateur à la même altitude à 250 m / s (900 km / h, 485 kt) par rapport à l'air environnant. (Gardez à l'esprit: pas de vent). En 24h, cet avion parcourt une distance de 21600 km, soit 0,539 de la circonférence. Cela signifie que l'avion effectue 1,539 tours de cercle en 24h, ce qui signifie que sa vitesse angulaire est $ \ omega = 1,539 \ cdot \ frac {2 \ pi} {24 \ cdot60 \ cdot60s} $. Ainsi, la force centrifuge sur l'avion voler vers l'est est

$$ a_ \ rm {ce} = 0,0799053814 m / s ^ 2 = 0,0081452988 g $$

De la même manière, on peut calculer ce qui se passe lorsque l'avion vole ouest: $ \ omega = (1-0,539) \ cdot \ frac {2 \ pi} {24 \ cdot60 \ cdot60s} $

$$ a_ \ rm {cw} = 0,0071833292 m / s ^ 2 = 0.0007322456 g $$

Comparaison

Écrivons les valeurs ensemble pour les comparer. J'ai également ajouté à quel point une personne de 100 kg (220 lb) serait plus légère en raison des effets:

  | "perte de poids" g_diff = 0,0368565736 m / s² = 0,003757 g | 376 grammes (0,829 lb) a_cb = 0,03374061 m / s² = 0,0034394098 g | 344 grammes (0,758 lb) a_ce = 0,0799053814 m / s² = 0,0081452988 g | 815 grammes (1,797lb) a_cw = 0,0071833292 m / s² = 0,0007322456 g | 73gram (0.161lb)  

Remarque: Les 100 kg sont ce que montre une balance au pôle Nord (c'est-à-dire sans effet centrifuge). La personne se sent déjà 344g plus légère au sol à l'équateur. Le ballon ne change pas (beaucoup) cela, mais le déplacement est / ouest a un effet plus important sur le poids que la gravité seule. Une personne qui vole vers l'ouest se sent encore plus lourde qu'au sol!

Peut-être un autre tableau, indiquant le poids de la personne:

  kg lb1. Homme au pôle nord 100,00 220,462. L'homme à l'équateur 99,66 219,703. Homme à l'équateur, en ballon 99,28 218,884. Homme à l'équateur, dans un avion volant vers l'est 98,81 217,84
5. Homme à l'équateur, dans un avion volant à l'ouest 99,55 219,47 <- Plus de 3.  

Les chiffres indiqués ne sont valables qu'à l'équateur et pour les vols est / ouest. Dans d'autres cas, cela devient un peu plus complexe.

MODIFIER: Étant curieux de savoir comment cela dépend de la latitude, j'ai créé ce graphique sur l'accélération absolue d'un avion.

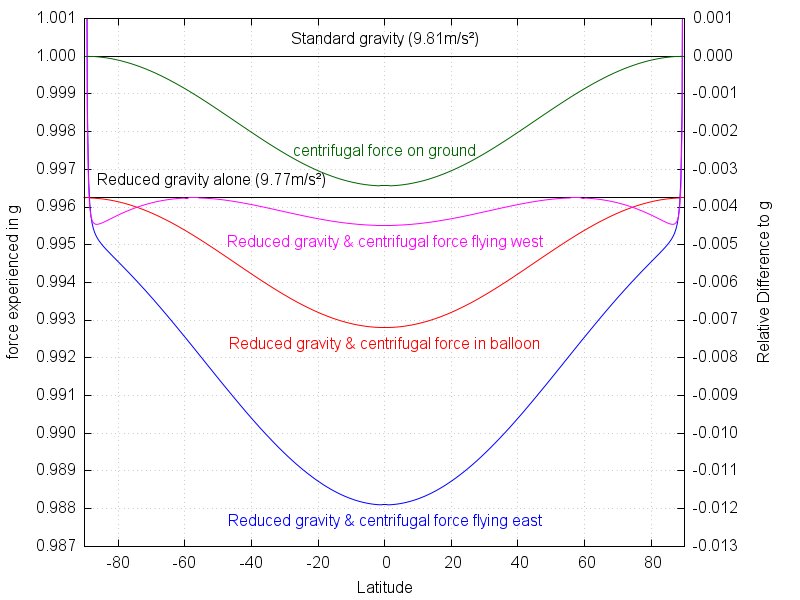
Le rayon dans l'équation de la force centrifuge est la distance de l'avion à l'axe de la Terre. Il est clair qu'elle diminue en s'éloignant de l'équateur, de même que l'accélération.

La vitesse de l'avion volant vers l'ouest annulera la vitesse de la Terre à environ 57 ° N / S, c'est-à-dire qu'il n'y a pas de force centrifuge. À une plus grande latitude, l'avion volera dans la direction opposée autour de l'axe de la terre, créant à nouveau une force centrifuge.
Près des pôles, les deux avions deviennent des centrifugeuses (théoriquement). Par exemple. voler sur un cercle de 500 m de rayon donne une accélération de 12,7 g. C'est pourquoi les données montent à l'infini là-bas.

(Lors du calcul, il faut garder à l'esprit que la gravité pointe toujours vers le centre de la terre, tandis que la force centrifuge s'éloigne de l'axe. Vous ne pouvez pas simplement les ajouter)

Vous avez raison de dire que la force de gravité est légèrement moindre à mesure que vous vous éloignez de la terre. Les compagnies aériennes naviguent généralement entre 30 000 et 35 000 pieds. Nous pouvons utiliser comme mesure approximative la force de gravité sur le mont. Everest, qui mesure 29 000 pieds.

La force de gravité sur l'Everest est d'environ 0,434% inférieure à la norme 9,8 N / kg. Cela signifie qu'une livre au niveau de la mer pèserait environ 0,995 livres. à 29 000 pieds. Ou, un humain typique de 180 livres pèserait 179,1 livres.

Je ne considère pas la vitesse de l'avion autour de la terre comme significative. Toute force centripète serait extrêmement petite.

Voici la version Estimation de Fermi, au cas où les calculs de la réponse d'Aeroalias seraient difficiles à suivre:

Il a été dit que l'ISS expérimente 0,9 G (90% de la gravité standard au niveau de la mer), qui est bien sûr annulée par leur vitesse orbitale pour que les astronautes à l'intérieur se sentent en 0G.

On dit que les avions volent à un mile de haut, et l'ISS est à plus de 100 miles high - ce ne sont pas des nombres particulièrement précis, mais ils sont assez bons pour des estimations d'ordre de grandeur.

Par conséquent, sans calculs compliqués, nous nous attendrions à ce qu'un avion subisse 99,9% de la gravité standard . Comme la réponse d'Aeroalias est de 99,63%, c'est une assez bonne estimation.

La gravité diminue avec l'altitude

Voir ce tableau indiquant la gravité à différentes altitudes:

^{Champ de gravité à différentes altitudes (source: The Engineering Toolbox)}

À une hauteur de 10 km, la gravité est de 9,776 contre 9.807 au niveau de la mer. C'est une variation de 0,32%, que je considère comme significative du point de vue de la conception de l'avion, car elle permet de réduire la consommation de carburant dans une plus grande proportion.

Peut-on sentir la différence de gravité à l'altitude de 10 km?

Une telle différence ne peut pas être détectée par un humain, un instrument de mesure est nécessaire. La détection d'une différence de 0,3% nécessite simplement une échelle. Si vous "pesez" une masse de 100 kg, alors à une hauteur de 10 km, la balance affichera juste 99,7 kg.

Remarque: Une valeur de gravité de 9,78 m / s² existe déjà sur Terre, par ex. à Mexico et à Singapour, en raison d ' anomalies de gravité.

À quelle vitesse la gravité diminue?

Le centre de gravité champ est près du centre de la Terre. La surface de la Terre est à 6400 km du centre et la valeur de la gravité est de 9,81 m / s² ou g.

Chaque fois que la distance du centre double, la valeur de la gravité est divisée par 4: À 12 800 km, la valeur est de 1/4 g. On dit que cette progression est une loi carrée inverse , qui ressemble à ceci:

^{Courbe d'une inverse loi carrée ( source)}

De nombreuses grandeurs physiques sont basées sur cette même loi (intensité lumineuse, intensité sonore, intensité du signal radio). Comme vous pouvez le voir après 3 ou 4 rayons terrestres, la variation a beaucoup ralenti, mais elle continue de diminuer et n'atteindra jamais zéro. cela signifie que tout objet de l'univers a un impact sur tous les autres objets! (mais petit).

La valeur de gravité diminue lors de l'escalade, mais aussi lors de la descente sous terre. Près du centre de la Terre la gravité est nulle (du moins c'est ce que nous croyons, nous n'allons pas pouvoir vérifier avant très longtemps, il est plus facile d'explorer l'espace que les profondeurs de notre planète). Voici le tableau complet de la gravité:

^{Champ de gravité selon le modèle terrestre de référence préliminaire sup>}

La gravité est une force déroutante qui n'est pas encore comprise. Nous connaissons les effets locaux de la gravité, mais nous ignorons les raisons de ces effets.

La plupart des questions portent sur la réduction de la gravité due à l'augmentation de la distance par rapport à la Terre, mais il existe également une force centrifuge causée par le mouvement. Cette force permet aux vaisseaux spatiaux de faire le tour de la Terre sans aucune puissance appliquée et provoque l'apesanteur à l'intérieur - une simple distance accrue ne serait pas suffisante pour ces effets. Un avion vole également autour de la Terre, comme le fait un satellite, mais beaucoup plus lentement.

Cet effet décrit ici et peut réduire le poids perçu (l'avion semble plus léger et tout à l'intérieur est plus léger) mais peut également l'augmenter (selon la façon dont la direction de vol est liée à la rotation de la Terre). L'effet est d'environ 0,3% de la masse à des vitesses proches de la vitesse du son, donc comparable à l'effet de l'augmentation de l'altitude.

La plupart des réponses ici sont du point de vue "à une hauteur de X, vous pesez Y". Permet de renverser la situation.

À l'altitude de l'ISS, la gravité est inférieure d'environ 10%. Je doute que vous remarquiez une réduction de poids de 10% (en double aveugle, si une telle chose était possible), sans utiliser d'appareil de mesure. Cela fait 400 km d'altitude, et bien en dehors de notre atmosphère.

La seule raison pour laquelle les gens sont en "apesanteur" sur l'ISS, c'est qu'ils sont en orbite.

Choses en orbite sont toujours en apesanteur. La balance sur laquelle vous vous tenez tombe à la même vitesse que vous. Cela peut se produire à n'importe quelle altitude - si vous frappez un ballon, il est en orbite - une orbite qui croise la surface de la Terre, de sorte qu'elle ne peut pas terminer l'orbite.